Prueba de corridas arriba y abajo: implementación en Java

La prueba de corridas arriba y abajo permite determinar si un conjunto de números pseudoaleatorios son independientes. En éste artículo explicamos esa prueba y su implementación en el lenguaje de programación Java.

Aprende a aplicar la Prueba de corridas

Prueba de corridas arriba y abajo

Escribir una cadena de ceros y unos.

Primero se recorre la lista de números pseudoaleatorios. Si el número i es menor o igual al número i-1 (el anterior), se anota un 0 (cero), de lo contrario se anota un 1.

Por ejemplo, en los siguientes 15 números:

0.6129, 0.7097, 0.9355, 0.7742, 0.7419, 0.3226, 0.0323, 0.3871, 0.8710, 0.9677, 0.1613, 0,

1, 0.5806, 0.2903   

Se observa que 0.6129 es menor que 0.7097, por lo que anotamos un 1.

Se observa que 0.7097 es menor que 0.9355, por lo que anotamos un 1.

Se observa que 0.9355 es mayor que 0.7742, por lo que anotamos un 0.

La cadena completa de unos y ceros quedaría así:

11000011100100

Contar las corridas

De la cadena anterior de ceros y unos, procedemos a contar las corridas. Si escribimos de nuevo la cadena separando los grupos de unos de los grupos de ceros, nos quedaría así:

11-0000-111-00-1-00

Vemos que hay 6 grupos de ceros o unos. Esos grupos se les llama corridas.

Corridas = 6

Cálculo de la media

Se calcula el valor esperado usando la siguiente formula:

Por lo que la media es:

Se calcula la varianza usando la siguiente fórmula:

Por lo que la varianza es:

Se obtiene el estadístico Z mediante la siguiente ecuación:

Por lo que el estadístico Z es:

Comparamos el valor obtenido del estadístico Z con el valor de la tabla de distribución normal para \alpha/2. Consideramos que \alpha es 0.05, es decir, utilizamos un índice de confianza de 95%, por lo que \alpha/2 es 0.025. El dato a buscar en la tabla de distribución normal es 1-0.025, esto es, 0.9750. El valor de Z en la tabla de distribución normal para 0.9750 es 1.96. Si el valor obtenido con la fórmula, es mayor al valor de la tabla, se concluye que los números no son independientes.

Como podemos observar, el valor del estadístico Z obtenido de la prueba de corridas al conjunto de 15 números pseudoaleatorios utilizado en este ejemplo es 2.39,  es mayor a 1.96 por lo que éste conjunto de números no pasa la prueba de corridas y no se puede afirmar que sean números independientes (por lo que no se deberían utilizar en un sistema de simulación).

Esto en parte se debe a que hay una cadena constante de ceros en la prueba:

11-0000-111-00-1-00

Esto ocurrió porque hay 4 números pseudoaleatorios que aparecen en forma decreciente. Esa clase de tendencia pueden hacer que un sistema de simulación no se comporte en forma aleatoria dando lugar a resultados no esperados.

Implementación en Java

Se propone la siguiente solución en el lenguaje Java:

Números a probar y variables a utilizar

static double datos[] = {
                         0.6129,
                         0.7097,
                         0.9355,
                         0.7742,
                         0.7419,
                         0.3226,
                         0.0323,
                         0.3871,
                         0.8710,
                         0.9677,
                         0.1613,
                         0,
                         1,
                         0.5806,
                         0.2903   
       };
    final static double confianza = .95;
    static  double alfa = 1-confianza;

Procedimiento

static public void pruebacorridas(){
    //Creamos una lista para guardar los ceros y unos.
    ArrayList<Integer> bits = new ArrayList<>();
    int i, corridas, dato;
    double  media, varianza, z;
    //Revisa si cada dato actual es menor al dato anterior. 
    //Si es así, se guarda un 0, de lo contrario, se guarda un 1
    for (i=1; i<datos.length; i++){
        if (datos[i]<=datos[i-1]){
            bits.add(0);
        }
        else{
            bits.add(1);
        }                
    }
    
    //Imprimimos la cadena de ceros y unos
    for (i=0; i<bits.size(); i++){
        System.out.print(bits.get(i));
    }

    //Contamos las corridas. 
    corridas = 1;
    //Comenzamos observando el primer dígito
    dato= bits.get(0);
    //Comparamos cada dígito con el observado, cuando cambia es 
    //una nueva corrida
    for (i=1; i<bits.size(); i++){
        if (bits.get(i) != dato){
            corridas++;
            dato = bits.get(i);
        }
    }
    System.out.println("Corridas " + corridas);
    
    //Aplicamos las fórmulas para media, varianza y Z.
    media = (2*datos.length-1)/ (double)3;
    System.out.println("Media: " +media);        
    varianza = (16*datos.length-29)/(double) 90;
    System.out.println("Varianza: " + varianza);
    z= Math.abs((corridas-media)/Math.sqrt(varianza));
    System.out.println("Z=" + z);     

    //Obtenemos el valor Z de la tabla de distribución normal
    NormalDistribution normal = new NormalDistribution();
    double  zn =  normal.inverseCumulativeProbability(1-alfa/2);
    //Comparamos: si es mayor mi valor Z al de la tabla, no pasa
    if (z < zn){
        System.out.println("No se rechaza que son independientes. " );
    }
    else{
        System.out.println("No Pasa la prueba de corridas");
    }
 
}

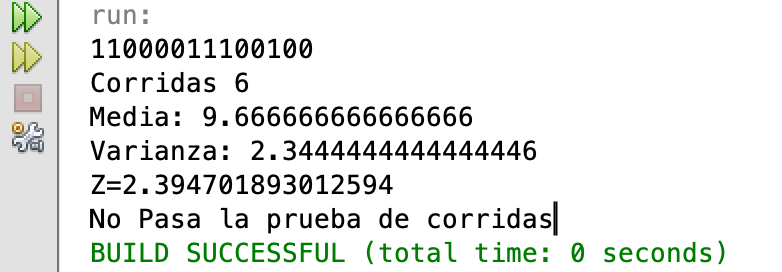
Ejecución

Prueba de corridas

Referencias

1. Dunna, E. G., Reyes, H. G., & Barrón, L. E. C. (2006). Simulación y análisis de sistemas con ProModel. Pearson Educación.

Cómo citar éste artículo

Si utilizas ésta información se agradece citar su fuente:

–>García, F. G (2019). Prueba de corridas arriba y abajo: implementación en Java. Disponible en [https://naps.com.mx/blog/prueba-de-corridas-en-java/] <–

Tu comentario

opiniones