Definición y origen de los números complejos
En este artículo consideramos qué son los números complejos y mencionamos el por qué de su surgimiento a partir de los números imaginarios en el siglo XVI.
Aprende más sobre números complejos
Definición de los números complejos
Un número complejo es un número escrito en la forma z= a + bi donde a y b son números reales e i es el símbolo formal que satisface la relación i² = -1. (Lay, 2001). i es entonces un número imaginario.
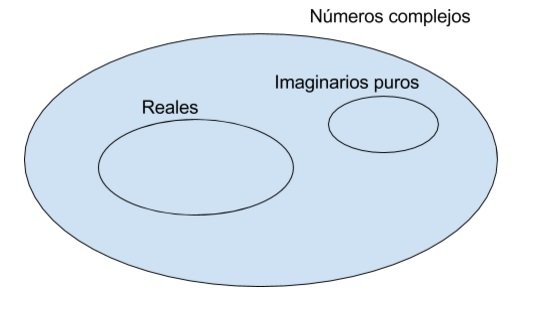
Si en z = a + bi, a = 0 se tiene un imaginario puro. Si b=0 se tiene un número real. (Flores y Fautsch, 1981). Los números complejos contienen a los números reales. Vea la siguiente figura.
Los números complejos contienen a los números reales
Las operaciones aritméticas con números reales pueden extenderse al conjunto de los números complejos.
Representación de números complejos
Veamos la representación puntual y la representación algebráica.
En una representación puntual, el número complejo z se representa como un punto del plano cartesiano (x,y) donde x es la parte real y y es la parte imaginaria.
En la representación algebráica se utiliza la forma ya mencionada z= a+bi
| Representación puntual | Representación algebráica |
| (3,4) | 3+4i |
| (-1,2) | -1+2i |
| (0,1) | 0+i = i |
| (2,0) | 2+0i = 2 |
| (4,-2) | 4+(-2i) = 4-2i |
Origen de los números complejos
En el siglo XVI la cantidad √-1 apareció por primera vez en la escena matemática (Mahor, 2006). Se le conoce como “unidad imaginaria” y se define como una de las soluciones de la ecuación x² + 1 = 0. Esta ecuación no admite soluciones reales, pues el cuadrado de todo número real es positivo. Procediendo formalmente se concluyó que i = √-1 es un número “imaginario” con derecho a existir en las matemáticas.
Posteriormente se formaron los objetos con la forma z= a + bi donde a y b son números reales, dando paso a los números complejos.
Una explicación detallada del desarrollo histórico de este tema los puedes encontrar en el prólogo de Funciones de una variable compleja de Guillermo Restrepo.
Referencias
- Flores y Fautsch (1981). Temas selectos de matemáticas. Editorial Progreso.
- Lay, David (2001). Algebra lineal y sus aplicaciones. Pearson Educación. México.
- Mahor E. (2006). e: historia de un número. Conaculta.
- Restrepo (2003). Funciones de una variable compleja. Universidad del valle.
Tu comentario
