Coeficiente de Jaccard en Python: Conjuntos en Python

Realizaremos una función que calcula el Coeficiente de Jaccard en Python, ésto nos servirá como un ejemplo del manejo de Conjuntos en Python.

Éste artículo también está disponible explicado en video, consúltalo aquí: https://youtu.be/oq7JWE04r4E

Conjuntos en Python

Los conjuntos son colecciones de elementos no ordenados ni indexados. Se identifican por utilizar llaves { }. Una vez creados los ítems, éstos no pueden ser modificados. Un conjunto no presenta elementos duplicados. (Chou, 2017)

Vamos a crear dos conjuntos:

grupo1 = {"john", "paul", "ringo", "george"}
grupo2 = {"john", "yoko", "eric", "ringo"}

Operaciones con conjuntos en Python

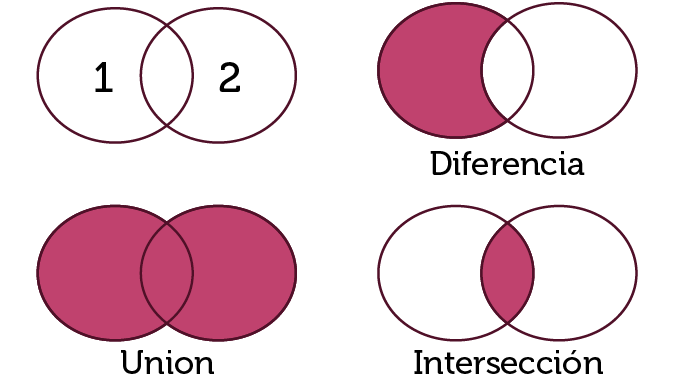
Considerando los conjuntos anteriores realizaremos las siguientes operaciones con conjuntos: pertenencia, unión, intersección, diferencia, diferencia simétrica e igualdad.

#Pertenencia
print ("ken" in grupo1)

#Unión
unidos = grupo1.union(grupo2)
print("Unión: ", unidos)

#Intersección
comunes = grupo1.intersection(grupo2)
print("Intersección: " , comunes)

#Diferencia
resta = grupo1 - grupo2
print("Diferencia: " , resta)

#Diferencia simétrica
difsim = grupo1.symmetric_difference(grupo2)
print("Dif. simétrica: " , difsim)

#Igualdad
grupo4 = {"juan", "miguel", "josefa"}
print ("Son iguales: " , grupo2 == grupo4)

La diferencia simétrica mostrará los elementos que están en un conjunto o en el otro, pero no en ambos.

Para que se considere a dos conjuntos iguales, éstos deben contener los mismos elementos.

Agregar y eliminar elementos de un conjunto

Para agregar un solo elemento se puede utilizar el método add. Si se desean agregar varios, debemos utilizar el método update. Para eliminar elementos podemos utilizar el método remove.

#Agregar un elemento
grupo2.add("billy")

#Remover un elemento
grupo2.remove("eric")
print("Agregar y remover: ", grupo2)

#Agregar varios elementos
grupo1.update(grupo2)
print ("Grupo1 nuevo: ", grupo1)

Ejemplo: Conjunto de letras en una palabra

Vamos a convertir una cadena a conjunto para analizar las letras que la conforman. Luego usaremos un for para recorrer el conjunto, mostrando elemento por elemento. Por ejemplo, la palabra ‘manzana’ tiene las letras ‘m’, ‘a’, ‘n’, y ‘z’, pues al momento de convertirla a conjunto eliminará los elementos repetidos.

#Que letras forman la palabra "manzana"
palabra = set("manzana")
for letra in palabra:
	print(letra)

Si ejecutas éste código varias veces observarás que en cada ejecución podría mostrarte un orden distinto. Esto es normal porque un conjunto es una colección de elementos no ordenados,  por lo que no se ‘garantiza’ que siempre aparezcan en el mismo orden.

Eliminar elementos repetidos en una lista usando conjuntos

Un conjunto no puede tener repetidos. Es posible escribir ésta línea en Python:

grupo3 = {“juan”, “juan”}

Pero al momento de imprimir el conjunto solo veremos un elemento ‘juan’.

Una lista sí puede tener repetidos. Y si por alguna razón deseamos eliminar esos elementos repetidos, podemos utilizar los conjuntos: convertir la lista a conjunto y, si se requiere, volver a convertir a lista.

#un set no puede tener repetidos 
grupo3 = {"juan", "juan"}
print ("Grupo 3: " ,grupo3)

#una lista si puede tener repetidos
grupo3 = ["juan", "juan", "maria"]
print ("Grupo 3 como lista: " , grupo3)

#es posible eliminar los repetidos de una lista convirtiendola a un set
print ("Eliminar repetidos: " , list(set(grupo3)))

Coeficiente de Jaccard en Python

El coeficiente de Jaccard es una medida de similitud entre dos grupos y se define como la cardinalidad de la intersección de ambos conjuntos dividida por la cardinalidad de su unión. Es muy usada para realizar sistemas de recomendación.  Por ejemplo, si dos usuarios tienen una lista de nombres de películas muy similar, pero no idéntica, podemos recomendarle a un usuario películas que no haya visto que estén en la lista del otro usuario.

def jaccard(grupo1, grupo2):
	interseccion = len(set(grupo1).intersection(set(grupo2)))
	union = len (set(grupo1).union(set(grupo2)))
	return interseccion / union

grupo_amigos1 = ["Manuel", "Rodrigo", "Miguel", "Jesus", "Irving"]
grupo_amigos2 = ["Manuel", "Alejandro", "Fernando", "Antonio", "Jesus", "Pablo"]

jacard_amigos = jaccard(grupo_amigos1, grupo_amigos2)
print ("Porcentaje de similitud: {:.2f}".format(jacard_amigos))

Los nombres están almacenados en listas, por lo que la función convertirá de listas a conjuntos. Se realiza la operación (ya sea intersección o unión) y se calcula la ‘cardinalidad’, es decir, cuántos elementos contiene el conjunto.

El resultado nos mostrará lo siguiente:

Mira éste artículo explicado en video:

Tu comentario

opiniones